Đạo động tuần hoàn là một chủ đề quan trọng trong môn Vật lý 11, nó giúp chúng ta hiểu về các khái niệm và ứng dụng của dao động trong cuộc sống hàng ngày. Trên cơ sở đó, chúng ta có thể áp dụng kiến thức về dao động tuần hoàn vào nhiều lĩnh vực khác nhau như cơ học, điện tử, và cả âm nhạc. Bài viết này sẽ giới thiệu về dao động tuần hoàn và những ứng dụng của nó.
1. Dao động tuần hoàn là gì?
Dao động tuần hoàn là dao động mà trạng thái chuyển động của vật được lặp lại như cũ sau những khoảng thời gian bằng nhau xác định.
Trong môn Vật lý 11, chúng ta thường học về hai loại dao động tuần hoàn quan trọng là dao động cơ và dao động điện từ.
Đạo động cơ là sự dao động của một vật thể quanh một vị trí cân bằng. Một ví dụ phổ biến về dao động cơ là dao động của một quả cầu treo trên một sợi dây. Khi quả cầu được kéo lệch khỏi vị trí cân bằng và thả tự do, nó sẽ dao động lên xuống. Quả cầu sẽ đi từ vị trí cao nhất, qua vị trí cân bằng và tiếp tục đi xuống đến vị trí thấp nhất. Quá trình này lặp đi lặp lại theo một chu kỳ nhất định. Đạo động cơ có nhiều ứng dụng thực tế, chẳng hạn như trong các chế độ rung của ô tô, trong các con lắc điện, và trong các thiết bị cơ khí khác.
Đạo động điện từ là sự dao động của một hệ thống do tương tác giữa điện và từ. Một ví dụ phổ biến về dao động điện từ là dao động của điện từ dòng xoay. Điện từ dòng xoay là một cuộn dây dẫn điện mắc nối tiếp với một cuộn cảm. Khi một dòng điện chạy qua cuộn dây, nó tạo ra một từ trường. Từ trường này tương tác với cuộn cảm, tạo ra một lực tác động trở lại cuộn dây. Lực này sẽ làm thay đổi dòng điện trong cuộn dây và quá trình này lặp đi lặp lại theo một chu kỳ nhất định. Đạo động điện từ có rất nhiều ứng dụng trong cuộc sống hàng ngày, chẳng hạn như trong các máy phát điện, máy biến áp, và các thiết bị điện tử khác.
2. Dao động tự do (dao động riêng), Chu kì, tần số của dao động
- Là dao động của hệ xảy ra dưới tác dụng chỉ của nội lực.
- Là dao động có tần số (tần số góc, chu kỳ) chỉ phụ thuộc các đặc tính của hệ không phụ thuộc các yếu tố bên ngoài. Khi đó: ω gọi là tần số góc riêng; f gọi là tần số riêng; T gọi là chu kỳ riêng.
Chu kì, tần số của dao động điều hòa
- Chu kì T của dao động điều hòa là khoảng thời gian để thực hiện một dao động toàn phần; đơn vị giây (s).
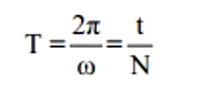
Với N là số dao động toàn phần vật thực hiện được trong thời gian t.
- Tần số f của dao động điều hòa là số dao động toàn phần thực hiện được trong một giây; đơn vị héc (Hz).
3. Dao động điều hòa là gì? Phương trình dao động điều hòa
Dao động điều hòa là dao động trong đó li đô (vị trí) của vật là một hàm côsin (hay sin) của thời gian.
Phương trình dao động điều hòa.
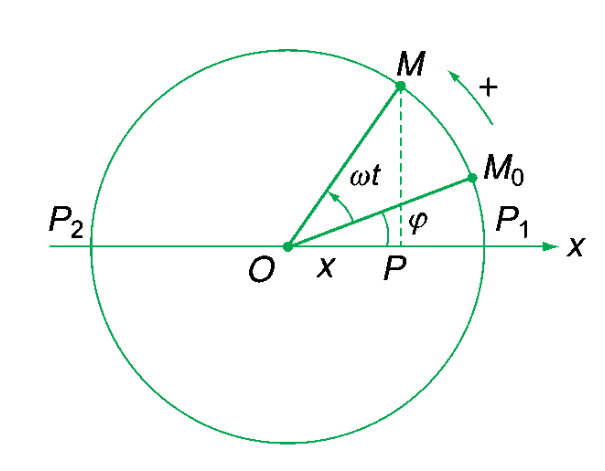
Điểm P dao động điều hòa trên một đoạn thẳng từ -A đến A luôn có thể coi là hình chiếu của một điểm M chuyển động tròn đều với tốc độ góc ω, trên đường tròn có đường kính là đoạn thẳng đó.
Chứng minh:
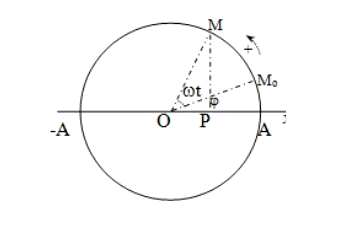
Giả sử t = 0 vật ở vị trí M0 được xác đinh bằng góc φ
Tại thời điểm t vị trí của M là (ωt + φ)
Khi đó hình chiều P của M có tọa độ :
x = A cos(ωt + φ)
Phương trình trên được gọi là phương trình của dao động điều hòa.
Trong đó:
x: Li độ của vật.
A: Biên độ của vật ( giá trị lớn nhất của li độ).
ω: tốc độ góc trong chuyển động tròn đều hay tần số góc trong dao động điều hòa.
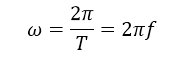
ωt + φ: pha dao động tại thời điểm t.
φ: pha ban đầu ( pha dao động tại thời điểm ban đầu).
4. Tìm li độ và hướng chuyển động
Vật chuyển động về vị trí cân bằng là nhanh dần (không đều) và chuyển động ra xa vị trí cân bằng là chậm dần (không đều).
Cách 1:
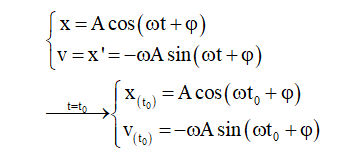
+ v(t0) > 0: Vật đi theo chiều dương (x đang tăng).
+ v(t0) < 0: Vật đi theo chiều âm (x đang giảm).
Cách 2:
Xác định vị trí trên vòng lượng giác ở thời điểm t0: ϕ = ωt0 + φ.
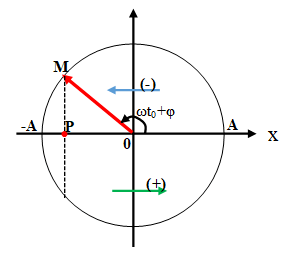
+ Hạ M xuống trục Ox ta được vị trí của vật ở thời điểm t0.
+ Nếu véctơ quay thuộc nửa trên vòng tròn lượng giác thì hình chiếu chuyển động theo chiều âm (li độ đang giảm).
+ Nếu véctơ quay thuộc nửa dưới vòng tròn lượng giác thì hình chiếu chuyển động theo chiều dương (li độ đang tăng).
Vậy li độ dao động điều hòa: x = A.cosϕ(t0) = A.cos(ωt0 + φ)
Vận tốc dao động điều hòa: v = x’ = -ωAsin ϕ(t0) = - ωAsin(ωt0 + φ).
Tóm lại, dao động tuần hoàn là một chủ đề quan trọng trong môn Vật lý 11. Nó giúp chúng ta hiểu về những khái niệm và ứng dụng của dao động trong các lĩnh vực khác nhau như cơ học, điện tử, và âm nhạc. Việc nắm vững kiến thức về dao động tuần hoàn sẽ giúp chúng ta áp dụng vào thực tế và khám phá những ứng dụng mới trong cuộc sống hàng ngày.