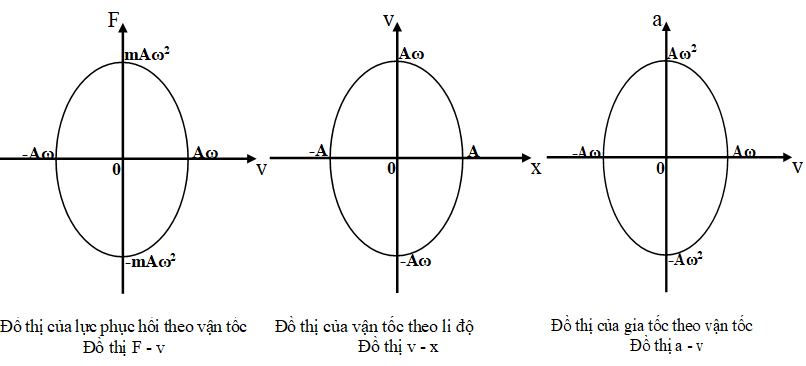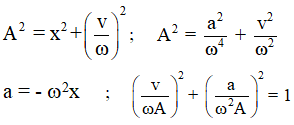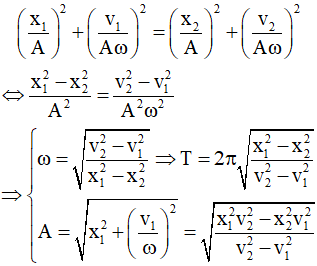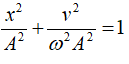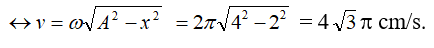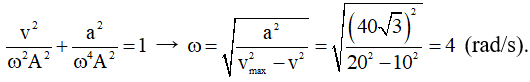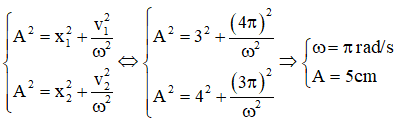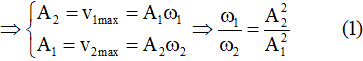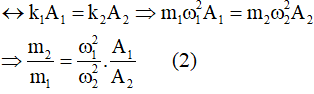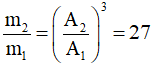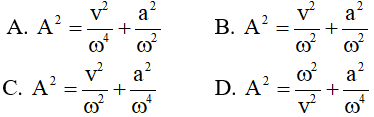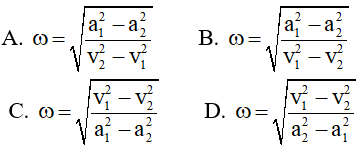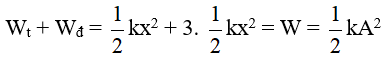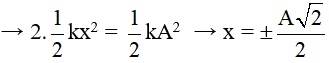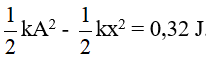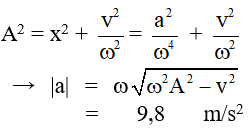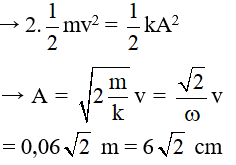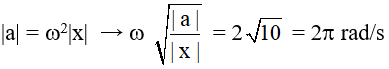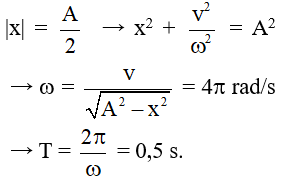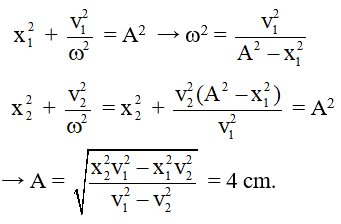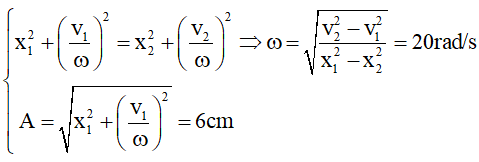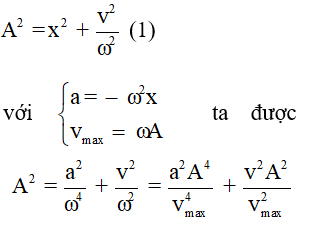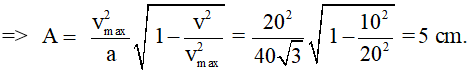A. Phương pháp & Ví dụ
1. Phương pháp
Dựa vào độ lệch pha giữa 2 đại lượng dao động điều hòa, ta thiết lập nên được mối quan hệ không phụ thuộc thời gian giữa chúng cho dưới bảng sau. Sử dụng các mối quan hệ này để giải quyết những bài toán tìm giá trị tức thời của x, v, a, F khi đã cho 1 trong các đại lượng x, v, a , F.
* Đồ thị biểu diễn các mối quan hệ độc lập với thời gian:
* Hệ thức độc lập:
Chú ý: Việc áp dụng các phương trình độc lập về thời gian sẽ giúp chúng ta giải toán vật lý rất nhanh, do đó, học sinh cần học thuộc dựa vào mối quan hệ của từng đại lượng trong các công thức với nhau và phải vận dụng thành thạo cho các bài toán xuôi ngược khác nhau.
Với hai thời điểm t1, t2 vật có các cặp giá trị x1, v1 và x2, v2 thì ta có hệ thức tính ω, A và T như sau:
* Vật ở VTCB: x = 0; |v|Max = ωA; |a|Min = 0.
Vật ở biên: x = ± A; |v|Min = 0; |a|Max = ω2A.
* Sự đổi chiều và đổi dấu của các đại lượng:
+ x, a và F đổi chiều khi qua VTCB, v đổi chiều ở biên.
+ x, a, v và F biến đổi cùng T, f và
2. Ví dụ
Ví dụ 1: Một vật dao động điều hòa với phương trình x = 4cos(2πt + π/2) cm. Khi vật có li độ x = 2 cm thì vật có tốc độ là bao nhiêu?
Lời giải:
Từ phương trình x = 4cos(2πt + π/2) cm, ta xác định được các đại lượng sau:
Biên độ A = 4 (cm), tốc độ góc ω = 2π (rad/s)
Khi x = 2 (cm), áp dụng hệ thức liên hệ ta được
Ví dụ 2: [ĐH - 2011] Một chất điểm dao động điều hòa trên trục Ox. Khi chất điểm đi qua vị trí cân bằng thì tốc độ của nó là 20 cm/s. Khi chất điểm có tốc độ là 10 cm/s thì gia tốc của nó có độ lớn là cm/s2. Biên độ dao động của chất điểm là
Lời giải:
Khi chất điểm qua VTCB thì có tốc độ cực đại vmax = Aω = 20 cm/s.
Áp dụng hệ thức độc lập thời gian:
→ Biên độ dao động của chất điểm là A = vmax/ω = 20/4 = 5 cm.
Ví dụ 3: Một vật nhỏ khối lượng 100 g dao động điều hòa dưới tác dụng của một lực kéo về F = –2cos(4πt + π/3) N. Lấy π2 = 10. Biên độ dao động của vật bằng
Lời giải:
Đổi m = 100 g = 0,1 kg.
Ta có ω = 4π rad/s, Fmax = 2 N
Do Fmax = mω2A → A = Fmax/(mω2) = 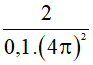
Ví dụ 4: Một vật dao động điều hòa: khi vật có li độ x1 = 3cm. Thì vận tốc là v1 = 4π cm/s, khi vật có li độ x2 = 4cm thì vận tốc là v2 = 3π cm/s. Tìm tần số góc và biên độ của vật?
Lời giải:
Từ các hệ thức độc lập với thời gian ta có:
Ví dụ 5: Cho hai vật dao động điều hòa trên hai đường thẳng song song với trục ox. Vị trí cân bằng của mỗi vật nằm trên đường thẳng vuông góc với ox tại O. Trong hệ trục vuông góc xov, đường (1) là đồ thị biểu diễn mối quan hệ giữa vận tốc và li độ của vật 1, đường (2) là đồ thị biểu diễn mối quan hệ giữa vận tốc và li độ của vật 2 (hình vẽ). Biết các lực kéo về cực đại tác dụng lên hai vật trong quá trình dao động là bằng nhau. Tỉ số giữa khối lượng của vật 2 với khối lượng của vật 1 là
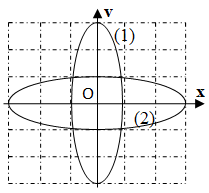
Lời giải:
Cách giải 1: Nhìn vào đồ thị ta thấy: A2 = 3A1
Theo giả thiết: Fphmax1 = Fphmax2
Từ (1) và (2), ta thu được:
Chọn đáp án C
Cách giải 2:
Từ đồ thị ta có:
Mặt khác:
B. Bài tập trắc nghiệm
Câu 1. Một vật dao động điều hòa có phương trình x = Acos(ωt + φ). Gọi v và a lần lượt là vận tốc và gia tốc của vật. Hệ thức đúng là.
Lời giải:
Chọn C
Câu 2. Một vật dao động điều hòa với tần số góc ω và biên độ B. Tại thời điểm t1 thì vật có li độ và tốc độ lần lượt là x1, v1, tại thời điểm t2 thì vật có li độ và tốc độ lần lượt là x2, v2. Tốc độ góc ω được xác định bởi công thức
Lời giải:
Chọn D
Câu 3. Một vật dao động điều hòa với tần số góc ω và biên độ B. Tại thời điểm t1 thì vật có li độ và tốc độ lần lượt là a1, v1, tại thời điểm t2 thì vật có li độ và tốc độ lần lượt là a2, v2. Tốc độ góc ω được xác định bởi công thức
Lời giải:
Chọn A
Câu 4. Một vật nhỏ dao động điều hòa trên trục Ox. Mốc thế năng tại vị trí cân bằng. Ở li độ x = 2 cm, vật có động năng gấp 3 lần thế năng. Biên độ dao động của vật là:
A. 6,0 cm B. 4,0 cm C. 3,5 cm D. 2,5 cm
Lời giải:
→ 4x2 = A2
→ A = 2x = 4 cm. Đáp án B
Câu 5. Một vật dao động điều hòa dọc theo trục Ox với chu kì T, vị trí cân bằng và mốc thế năng ở gốc tọa độ. Tính từ lúc vật có li độ dương lớn nhất, thời điểm đầu tiên mà động năng và thế năng của vật bằng nhau là:
A. T/4 B. T/8 C. T/12 D. T/6
Lời giải:
Khi Wt = Wđ thì 2Wt = W
khoảng thời gian ngắn nhất để vật đi từ vị trí có li độ A đến vị trí có li độ 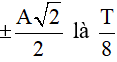
Câu 6. Một con lắc lò xo gồm viên bi nhỏ và lò xo nhẹ có độ cứng 100 N/m, dao động điều hòa với biên độ 0,1 m. Mốc thế năng ở vị trí cân bằng. Khi viên bi cách vị trí cân bằng 6 cm thì động năng của con lắc bằng
A. 0,64 J B. 3,2 mJ C. 6,4 mJ D. 0,32 J
Lời giải:
Wđ = W – Wt =
Đáp án D.
Câu 7. Một vật đang dao động điều hòa với tần số góc 10π rad/s và biên độ √2 cm. Khi vật có vận tốc 10√10 cm/s thì gia tốc của nó có độ lớn:
A. 4 m/s2 B. 10 m/s2 C. 2 m/s2 D. 5 m/s2.
Lời giải:
Đáp án B
Câu 8. Một con lắc lò xo gồm lò xo nhẹ và vật nhỏ dao động điều hòa theo phương ngang với tần số góc 10 rad/s. Biết khi động năng và thế năng (mốc ở vị trí cân bằng của vật) bằng nhau thì vận tốc của vật có độ lớn bằng 0,6 m/s. Biên độ dao động của con lắc là:
A. 6 cm B. 6√2 cm C. 12 cm D. 12√2 cm
Lời giải:
Khi Wđ = Wt thì Wt + Wđ = 2Wđ = W
Đáp án B
Câu 9. Một con lắc lò xo dao động điều hòa với chu kì T và biên độ 5 cm. Biết trong một chu kì, khoảng thời gian để vật nhỏ của con lắc có độ lớn gia tốc không vượt quá 100 cm/s2 là T/3. Lấy π2 = 10. Tần số dao động của vật là:
A. 4 Hz B. 3 Hz C. 1 Hz D. 2 Hz
Lời giải:
Trong 1/4 chu kì thời gian để độ lớn gia tốc không vượt quá 100 cm/s2 là T/12. Càng gần vị trí cân bằng thì gia tốc có độ lớn càng nhỏ nên sau khoảng thời gian T/12 kể từ vị trí cân bằng vật có độ lớn li độ |x| = A/2 = 2,5 cm. Khi đó
→ f = ω/2π = 1 Hz
Đáp án C
Câu 10. Một chất điểm dao động điều hòa trên trục Ox. Khi chất điểm đi qua vị trí cân bằng thì tốc độ của nó là 20 cm/s. Khi chất điểm có tốc độ là 10 cm/s thì gia tốc của nó có độ lớn là 40√3 cm/s2. Biên độ dao động của chất điểm là:
A. 5 cm B. 4 cm C. 10 cm D. 8 cm
Lời giải:
Đáp án A
Câu 11. Một chất điểm dao động điều hòa với chu kì T và biên độ 10 cm. Biết trong một chu kì, khoảng thời gian để chất điểm có vận tốc không vượt quá 20π√3 cm/s là 2T/3. Chu kì dao động của chất điểm là:
A. 3 s B. 2 s C. 1 s D. 0,5 s
Lời giải:
Trong 1/4 chu kỳ khoảng thời gian để chất điểm có vận tốc không vượt quá 20π√3 cm/s là T/6. Càng gần vị trí biên thì vận tốc của vật càng nhỏ nên sau khoảng thời gian T/6 kể từ vị trí biên vật có
Đáp án D
Câu 12. Một vật dao dao động điều hòa với p.trình x = Acos(ωt + φ). Tại các vị trí có li độ x1 = 2 cm và x2 = 2 cm, vật có vận tốc tương ứng là v1 = 20π√3 cm/s và v2 = 20π√2 cm/s. Biên độ dao động của vật có giá trị nào sau đây?
A. 4 cm B. 6 cm C. 4 cm D. 6 cm
Lời giải:
Đáp án A
Câu 13. Một vật nhỏ dao động điều hòa theo phương trình x = Acos4πt (t tính bằng s). Tính từ t = 0; khoảng thời gian ngắn nhất để gia tốc của vật có độ lớn bằng một nửa độ lớn gia tốc cực đại là:
A. 0,083 s B. 0,104 s C. 0,167 s D. 0,125s
Lời giải:
T = 2π/ω = 0,5 s; khi t = 0 thì x = A và a = amax
Sau thời gian ngắn nhất Δt = T/6 = 0,083 s thì x = A/2 và a = amax/2. Đáp án A
Câu 14. Một chất điểm dao động điều hòa. Tại thời điểm t1 li độ của chất điểm bằng x1 = 3 cm và vận tốc bằng v1 = - 60√3 cm/s. Tại thời điểm t2 li độ bằng x2 = -3√2 cm và vận tốc bằng v2 = -60√2 cm/s. Biên độ và tần số góc dao động của chất điểm lần lượt bằng:
A. 6 cm; 12 rad/s B. 12 cm; 10 rad/s
C. 6 cm; 20 rad/s D. 12 cm; 20 rad/s
Lời giải:
Ta có:
Câu 15. Một chất điểm dao động điều hòa trên trục Ox. Khi chất điểm đi qua vị trí cân bằng thì tốc độ của nó là 20 cm/s. Khi chất điểm có tốc độ là 10 cm/s thì gia tốc của nó có độ lớn là 40√3 cm/s2. Biên độ dao động của chất điểm
A. 5 cm B. 4 cm C. 10 cm D. 8 cm
Lời giải:
Từ công thức:
Đáp án A